Mixing liquids is easy: Pour milk into your coffee cup, and the mixing is immediate. Except this does not work so well at the microfluidic level. In fact, this does not work at all.

It is very hard to mix liquids in microchannels, as the physical phenomena that homogenizes fluids in an everyday-sized recipient’s drink (your coffee cup for example) are totally ineffective at the microfluidic channel level. Liquid flows in micro-channels are laminar. The chaotic eddies that homogenize fluids in turbulent flows are completely absent in a laminar flow. Rather, fluids follow smooth streamlines, which remain side-by-side even in meandering channels. There is little mixing between streamlines, so two fluids flowing in a standard microchannel will not mix with each other, except via a very slow diffusion at their common interface.

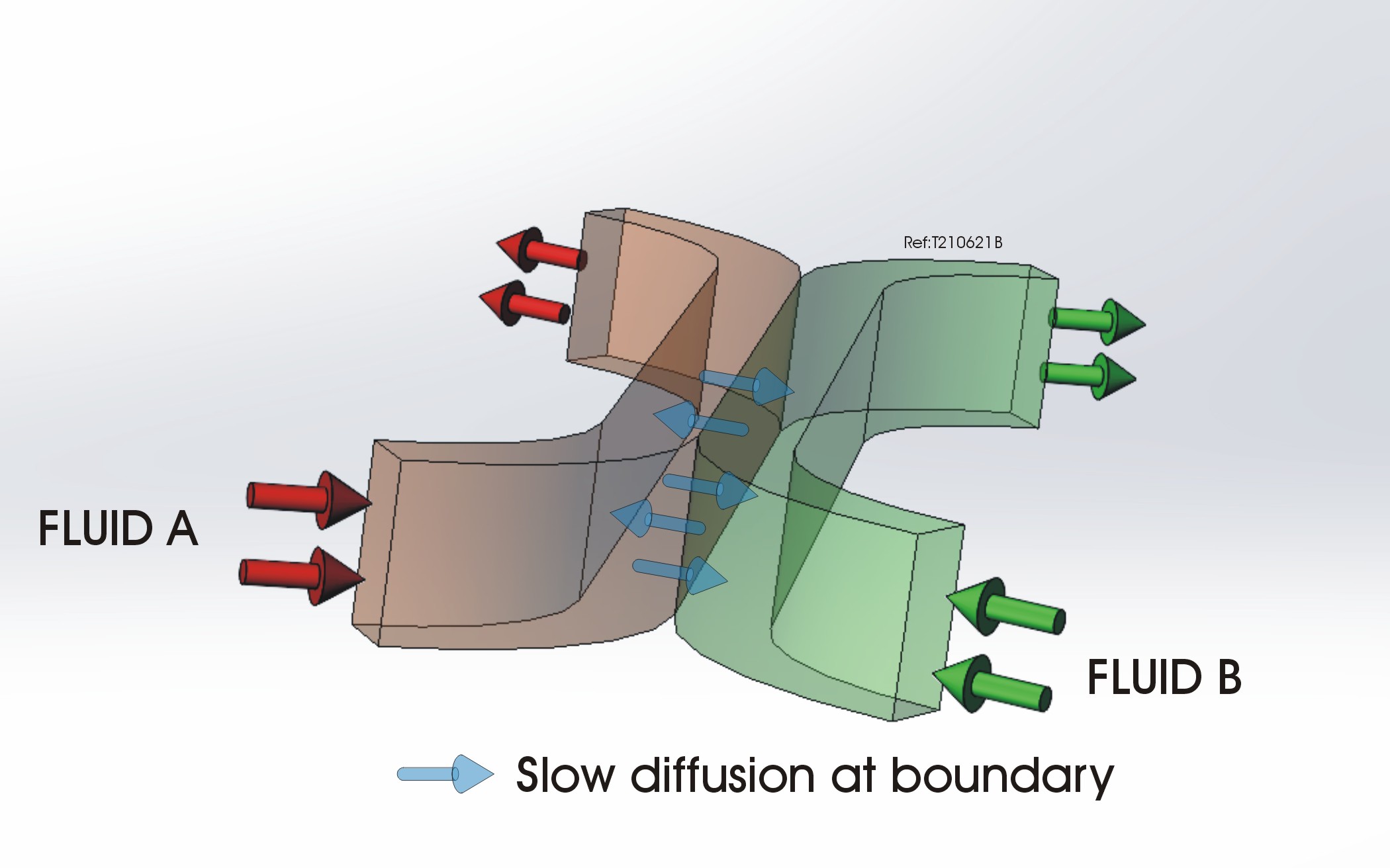
So, how can you efficiently mix fluids in microfluidic channels? 

• Increasing the fluids speed won’t help, except if you can reach the turbulent regime, which is very unlikely in a small channel (the smaller the channel the harder).
• Reducing a lot the fluids speed could help, as this would give more time for the diffusion to take place at the interface between the two fluids, but you would have to slow the flow so much that your sample would take days to go through your microfluidic chip. That is probably not what you want.
• Alternatively, one can reduce the diffusion length and increase the interface (i.e., the contact surface between the two liquids). One could implement this concept using a microfluidic channel that is very narrow and long. However, there are practical considerations (prevention of blockage, minimum flow requirement, etc.) that preclude drastically reducing the microfluidic channel width. A solution proposed by Whiteside [1] takes these shortcomings into consideration. Using small angled features, such as slots, ridges, or chevrons, one can generate transverse flow motions that effectively reduce the diffusion length and increase the contact surface between the liquids.

Let’s look in more detail how this type of passive microfluidic mixer works.  We start by looking at a simple case where one places angled grooves (or ridges) on the microfluidic channel floor (or ceiling [2]).By applying a (longitudinal) pressure gradient, one pushes the fluid down the microfluidic channel.  When the fluid encounters an angled groove, a transverse flow component is generated, as there is less resistance to the flow in the direction parallel to the groove.  As a result, the fluid will start to follow helical streamlines, slowly rotating along the longitudinal axis of the channel.

This mixing process can be further enhanced by replacing the angled groves with an asymmetrical chevron (or herringbone) pattern.  If two fluids are present, they end up being interlayered, which reduces the diffusion length.

The resulting mixed flow is not chaotic in the sense generally associated with turbulent flows.  In fact, it is deterministic: the mixing introduced by a given sequence of grooves or chevrons can be reversed using an inverse sequence, as has been beautifully demonstrated by the Ligler group [3, 4].

Even better mixing is obtained by periodically reversing the chevron asymmetry.  These patterns of chevrons can be repeated until an arbitrarily high degree of mixing is achieved.

References:

1. “Chaotic Mixer for Microchannel”, Abraham D. Stroock, Stephan K. W. Dertinger, Armand Ajdari, Igor Mezic, Howard A. Stone, George M. Whitesides, Science, 647 (2002).
2. “A microfluidic mixer with grooves placed on the top and bottom of the channel”, Peter B. Howell et al., Lab Chip, 524–530, (2005).
3. “Dynamic reversibility of hydrodynamic focusing for recycling sheath fluid”, Nastaran Hashemi, Peter B. Howell, Jr., Jeffrey S. Erickson, Joel P. Golden and Frances S. Ligler, Lab Chip, 1952–1959, (2010).
4. “A combinatorial approach to microfluidic mixing “,Howell, P.B., D.R. Mott, F.S. Ligler, J.P. Golden, C.R. Kaplan, and E.S. Oran, Micromech. Microeng. 18, 115019(1) – 115019(7). (2008).